数値シミュレーション－各解法の誤差比較－

数値シミュレーション解説第6回

カテゴリ:

シミュレーション

タグ:

シミュレーション数学

Published: 8/18/2018

Updated: 12/23/2025

約10分

数値シミュレーション解説の前回の記事

数値シミュレーション－ルンゲ＝クッタ法－

数値シミュレーション解説の次回の記事

数値シミュレーション－二重振り子－

【更新履歴】

2025/12/23: プログラムを C# 14.0 に修正

こんにちは、Rafkaです。今回は、今まで紹介してきた数値解法の誤差比較を、斜方投射を題材に行っていきます。

問題設定

斜方投射は以下の図のように、よく高校で習うような一般的な形でモデル化しました。

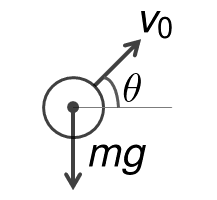
この時の位置に関する厳密解は、初期位置が

\boldsymbol{p}(0) = [p_x(0), p_y(0)]^\text{T} = [0, 0]^\text{T}

ならば、以下のようになります。

\begin{split} p_x(t) &= v_0t\cos(\theta) \\ p_y(t) &= v_0t\sin(\theta)-\frac{1}{2}gt^2 \end{split}

各数値解法による値と、この厳密解の値とを比較することで、どの程度誤差が発生しているのかを見ていきます。

厳密解が既に分かっているこの問題ですが、オイラー法等の数値解法でのシミュレーションのためには、微分方程式で表現されたモデルが必要なので、今回はあえて、ニュートンの運動方程式から出発して微分方程式によるモデル化を行います。

ニュートンの運動方程式より、以下の関係が成り立ちます。

m\boldsymbol{a}(t) = \boldsymbol{F}(t) = [0, -mg]^\text{T}

ここで、

{}^\text{T}

は行列の転置を表しています。上で時間

t

での位置を

\boldsymbol{p}(t)

と表したので、加速度

\boldsymbol{a}(t)

について以下の式が成り立ちます。

\boldsymbol{a}(t) = \frac{d^2\boldsymbol{p}(t)}{dt^2} = \frac{d\boldsymbol{v}(t)}{dt}

ですので、上で示した関係式は以下のように変形できます。

\frac{d^2\boldsymbol{p}(t)}{dt^2} = [0, -g]^\text{T}

ちゃっかり

m

で割ってます。

このままでは 2 階微分の方程式になってしまうので、

\frac{d\boldsymbol{p}(t)}{dt} = \boldsymbol{v}(t)

であることを利用して、以下のように 1 階微分の方程式に変形します。

\left\{ \begin{align*} \frac{d\boldsymbol{v}(t)}{dt} &= [0, -g]^\text{T} \\ \frac{d\boldsymbol{p}(t)}{dt} &= \boldsymbol{v}(t) = [v_x(t), v_y(t)]^\text{T} \end{align*} \right.

更にここで、

\boldsymbol{x}(t) = [\boldsymbol{v}(t), \boldsymbol{p}(t)]^\text{T} = [v_x(t), v_y(t), p_x(t),p_y(t)]^\text{T}

とすることで、以下のように一纏めにしてしまいます。

\frac{d\boldsymbol{x}(t)}{dt} = [0, -g, v_x(t), v_y(t)]^\text{T}

これで微分方程式を用いた斜方投射のモデル化が完了しました。

プログラム

斜方投射のシミュレーションを行うために、以下のようなプログラムにしてみました。

#!/usr/bin/dotnet run
 
var g = 9.81;
var vNorm = 5.0;
var angle = Math.PI / 4.0;
 
var result = Simulate(
  (x, _, dx) => { dx[0] = 0; dx[1] = -g; dx[2] = x[0]; dx[3] = x[1]; },
  stackalloc double[] { vNorm * Math.Cos(angle), vNorm * Math.Sin(angle), 0.0, 0.0 },
  Euler,
  0.1,
  10
);
 
foreach (var item in result) {
  Console.WriteLine($"Time={item[0]:F2} X={item[3]:F4} Y={item[4]:F4}");
}
 
void Euler(ModelFunction f, Span<double> x, double t, double dt) {
  var n = x.Length;
  Span<double> dx = stackalloc double[n];
 
  f(x, t, dx);
  ScaleAdd(x, dx, dt, x);
}
 
void Heun(ModelFunction f, Span<double> x, double t, double dt) {
  var n = x.Length;
 
  Span<double> k1 = stackalloc double[n];
  Span<double> k2 = stackalloc double[n];
  Span<double> tempX = stackalloc double[n];
 
  f(x, t, k1);
  ScaleAdd(x, k1, dt, tempX);
  f(tempX, t + dt, k2);
 
  for (var i = 0; i < n; i++) {
    var slope = (k1[i] + k2[i]) * 0.5;
    x[i] += slope * dt;
  }
}
 
void RungeKutta(ModelFunction f, Span<double> x, double t, double dt) {
  var n = x.Length;
 
  Span<double> k1 = stackalloc double[n];
  Span<double> k2 = stackalloc double[n];
  Span<double> k3 = stackalloc double[n];
  Span<double> k4 = stackalloc double[n];
  Span<double> tempX = stackalloc double[n];
 
  var halfDt = dt * 0.5;
 
  f(x, t, k1);
 
  ScaleAdd(x, k1, halfDt, tempX);
  f(tempX, t + halfDt, k2);
 
  ScaleAdd(x, k2, halfDt, tempX);
  f(tempX, t + halfDt, k3);
 
  ScaleAdd(x, k3, dt, tempX);
  f(tempX, t + dt, k4);
 
  for (var i = 0; i < n; i++) {
    var slope = k1[i] + 2.0 * k2[i] + 2.0 * k3[i] + k4[i];
    x[i] += slope * (dt / 6.0);
  }
}
 
List<double[]> Simulate(ModelFunction model, Span<double> state, SolverFunction solver, double dt, int steps) {
  var n = state.Length;
  var list = new List<double[]>();
 
  list.Add([0, ..state]);
  for (var i = 0; i < steps; i++) {
    var t = i * dt;
    solver(model, state, t, dt);
    list.Add([t + dt, ..state]);
  }
 
  return list;
}
 
delegate void ModelFunction(ReadOnlySpan<double> x, double t, Span<double> dx);
delegate void SolverFunction(ModelFunction model, Span<double> x, double t, double dt);

3 行目から 5 行目で、重力加速度

g

、初速度の大きさ

v_0

、発射角

\theta

を定義しています。 7 行目の Simulate メソッドでシミュレーションを実行しており、 8 行目のラムダ式で、先程示した微分方程式を実装しています。 9 行目で初期値を設定しており、 10 行目で使用する数値解法を指定しています。 11 行目と 12 行目で、時間刻み幅とステップ数を指定しています。

実行すると、選択した解法による各時間での位置が出力されます。

実行結果

実行した結果をグラフにプロットしました。今回のグラフは"再生"ボタンを押すことで、各時間までの軌跡を描きながらアニメーションする機能や、シークバーを動かして指定した時間までの軌跡を描画することができるので、是非遊んでみてください。

斜方投射シミュレーション

結果を見てみると、オイラー法の結果は厳密解から大きく外れてしまっている事が分かります。一方で、ホイン法やルンゲ＝クッタ法の結果は厳密解と同じ軌跡を辿っており、これらの手法の精度の高さを確認できると思います。ホイン法とルンゲ＝クッタ法の精度の差を見ることが難しい結果となってしまいましたが、これは時間刻みをより荒くした時に顕著に確認できます。